Optimization of model parameters via simulated annealing

tune_sim_anneal() uses an iterative search procedure to generate new candidate tuning parameter combinations based on previous results. It uses the generalized simulated annealing method of Bohachevsky, Johnson, and Stein (1986).

Usage

tune_sim_anneal(object, ...)

# S3 method for model_spec
tune_sim_anneal(
  object,
  preprocessor,
  resamples,
  ...,
  iter = 10,
  param_info = NULL,
  metrics = NULL,
  eval_time = NULL,
  initial = 1,
  control = control_sim_anneal()
)

# S3 method for workflow
tune_sim_anneal(
  object,
  resamples,
  ...,
  iter = 10,
  param_info = NULL,
  metrics = NULL,
  eval_time = NULL,
  initial = 1,
  control = control_sim_anneal()
)

Arguments

object: A parsnip model specification or a workflows::workflow().
...: Not currently used.
preprocessor: A traditional model formula or a recipe created using recipes::recipe(). This is only required when object is not a workflow.
resamples: An rset() object.
iter: The maximum number of search iterations.
param_info: A dials::parameters() object or NULL. If none is given, a parameter set is derived from other arguments. Passing this argument can be useful when parameter ranges need to be customized.
metrics: A yardstick::metric_set() object containing information on how models will be evaluated for performance. The first metric in metrics is the one that will be optimized.
eval_time: A numeric vector of time points where dynamic event time metrics should be computed (e.g. the time-dependent ROC curve, etc). The values must be non-negative and should probably be no greater than the largest event time in the training set (See Details below).
initial: An initial set of results in a tidy format (as would the result of tune_grid(), tune_bayes(), tune_race_win_loss(), or tune_race_anova()) or a positive integer. If the initial object was a sequential search method, the simulated annealing iterations start after the last iteration of the initial results.
control: The results of control_sim_anneal().

Value

A tibble of results that mirror those generated by tune_grid(). However, these results contain an .iter column and replicate the rset

object multiple times over iterations (at limited additional memory costs).

Details

Simulated annealing is a global optimization method. For model tuning, it can be used to iteratively search the parameter space for optimal tuning parameter combinations. At each iteration, a new parameter combination is created by perturbing the current parameters in some small way so that they are within a small neighborhood. This new parameter combination is used to fit a model and that model's performance is measured using resampling (or a simple validation set).

If the new settings have better results than the current settings, they are accepted and the process continues.

If the new settings has worse performance, a probability threshold is computed for accepting these sub-optimal values. The probability is a function of how sub-optimal the results are as well as how many iterations have elapsed. This is referred to as the "cooling schedule" for the algorithm. If the sub-optimal results are accepted, the next iterations settings are based on these inferior results. Otherwise, new parameter values are generated from the previous iteration's settings.

This process continues for a pre-defined number of iterations and the overall best settings are recommended for use. The control_sim_anneal() function can specify the number of iterations without improvement for early stopping. Also, that function can be used to specify a restart threshold; if no globally best results have not be discovered within a certain number if iterations, the process can restart using the last known settings that globally best.

Creating new settings

For each numeric parameter, the range of possible values is known as well as any transformations. The current values are transformed and scaled to have values between zero and one (based on the possible range of values). A candidate set of values that are on a sphere with random radii between rmin and rmax are generated. Infeasible values are removed and one value is chosen at random. This value is back transformed to the original units and scale and are used as the new settings. The argument radius of control_sim_anneal() controls the range neighborhood sizes.

For categorical and integer parameters, each is changes with a pre-defined probability. The flip argument of control_sim_anneal() can be used to specify this probability. For integer parameters, a nearby integer value is used.

Simulated annealing search may not be the preferred method when many of the parameters are non-numeric or integers with few unique values. In these cases, it is likely that the same candidate set may be tested more than once.

Cooling schedule

To determine the probability of accepting a new value, the percent difference in performance is calculated. If the performance metric is to be maximized, this would be d = (new-old)/old*100. The probability is calculated as p = exp(d * coef * iter) were coef is a user-defined constant that can be used to increase or decrease the probabilities.

The cooling_coef of control_sim_anneal() can be used for this purpose.

Termination criterion

The restart counter is reset when a new global best results is found.

The termination counter resets when a new global best is located or when a suboptimal result is improved.

Parallelism

The tune and finetune packages currently parallelize over resamples. Specifying a parallel back-end will improve the generation of the initial set of sub-models (if any). Each iteration of the search are also run in parallel if a parallel backend is registered.

Censored regression models

With dynamic performance metrics (e.g. Brier or ROC curves), performance is calculated for every value of eval_time but the first evaluation time given by the user (e.g., eval_time[1]) is used to guide the optimization.

Also, values of eval_time should be less than the largest observed event time in the training data. For many non-parametric models, the results beyond the largest time corresponding to an event are constant (or NA).

References

Bohachevsky, Johnson, and Stein (1986) "Generalized Simulated Annealing for Function Optimization", Technometrics, 28:3, 209-217

Examples

# \donttest{
library(finetune)
library(rpart)
#> 
#> Attaching package: ‘rpart’
#> The following object is masked from ‘package:dials’:
#> 
#>     prune
library(dplyr)
#> 
#> Attaching package: ‘dplyr’
#> The following object is masked from ‘package:MASS’:
#> 
#>     select
#> The following objects are masked from ‘package:stats’:
#> 
#>     filter, lag
#> The following objects are masked from ‘package:base’:
#> 
#>     intersect, setdiff, setequal, union
library(tune)
library(rsample)
library(parsnip)
library(workflows)
library(ggplot2)

## -----------------------------------------------------------------------------
if (rlang::is_installed("modeldata")) {
  data(two_class_dat, package = "modeldata")

  set.seed(5046)
  bt <- bootstraps(two_class_dat, times = 5)

  ## -----------------------------------------------------------------------------

  cart_mod <-
    decision_tree(cost_complexity = tune(), min_n = tune()) %>%
    set_engine("rpart") %>%
    set_mode("classification")

  ## -----------------------------------------------------------------------------

  # For reproducibility, set the seed before running.
  set.seed(10)
  sa_search <-
    cart_mod %>%
    tune_sim_anneal(Class ~ ., resamples = bt, iter = 10)

  autoplot(sa_search, metric = "roc_auc", type = "parameters") +
    theme_bw()

  ## -----------------------------------------------------------------------------
  # More iterations. `initial` can be any other tune_* object or an integer
  # (for new values).

  set.seed(11)
  more_search <-
    cart_mod %>%
    tune_sim_anneal(Class ~ ., resamples = bt, iter = 10, initial = sa_search)

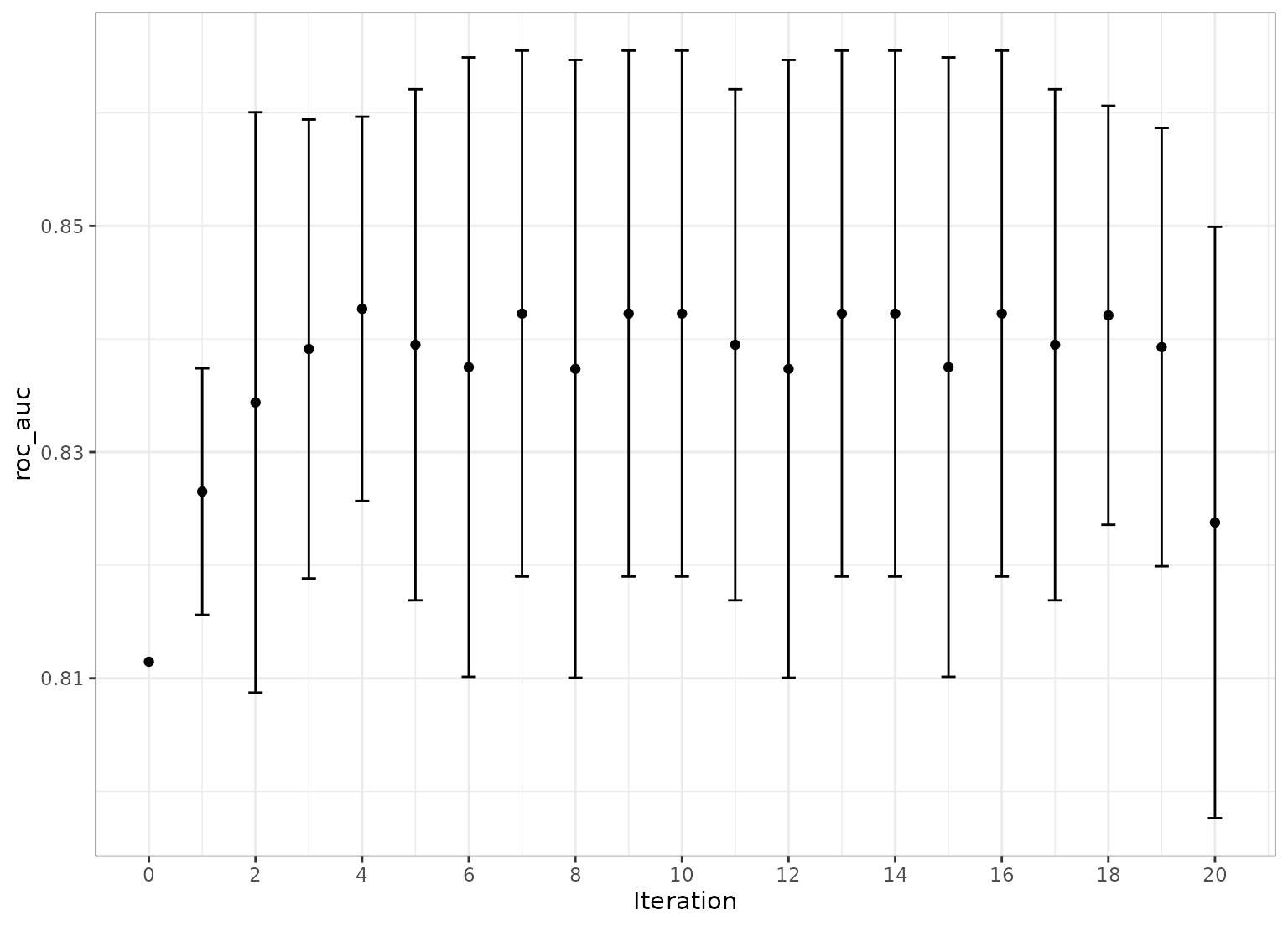
  autoplot(more_search, metric = "roc_auc", type = "performance") +
    theme_bw()
}
#> Optimizing roc_auc
#> Initial best: 0.81147
#> 1 ♥ new best           roc_auc=0.82651 (+/-0.004242)
#> 2 ♥ new best           roc_auc=0.83439 (+/-0.009983)
#> 3 ♥ new best           roc_auc=0.83912 (+/-0.007893)
#> 4 ♥ new best           roc_auc=0.84267 (+/-0.006609)
#> 5 ◯ accept suboptimal  roc_auc=0.83949 (+/-0.008792)
#> 6 ◯ accept suboptimal  roc_auc=0.83751 (+/-0.01065)
#> 7 + better suboptimal  roc_auc=0.84225 (+/-0.009044)
#> 8 ◯ accept suboptimal  roc_auc=0.83736 (+/-0.01063)
#> 9 + better suboptimal  roc_auc=0.84225 (+/-0.009044)
#> 10 ◯ accept suboptimal  roc_auc=0.84225 (+/-0.009044)
#> There were 10 previous iterations
#> Optimizing roc_auc
#> 10 ✔ initial            roc_auc=0.84267 (+/-0.006609)
#> 11 ◯ accept suboptimal  roc_auc=0.83949 (+/-0.008792)
#> 12 ◯ accept suboptimal  roc_auc=0.83736 (+/-0.01063)
#> 13 + better suboptimal  roc_auc=0.84225 (+/-0.009044)
#> 14 ◯ accept suboptimal  roc_auc=0.84225 (+/-0.009044)
#> 15 ◯ accept suboptimal  roc_auc=0.83751 (+/-0.01065)
#> 16 + better suboptimal  roc_auc=0.84225 (+/-0.009044)
#> 17 ◯ accept suboptimal  roc_auc=0.83949 (+/-0.008792)
#> 18 ✖ restart from best  roc_auc=0.8421 (+/-0.007206)
#> 19 ◯ accept suboptimal  roc_auc=0.83928 (+/-0.007538)
#> 20 ─ discard suboptimal roc_auc=0.82378 (+/-0.01017)

# }